Zooming

This problem was asked in a shared server around 4 years ago, and I solved it together with some others. It's quite an interesting exercise!

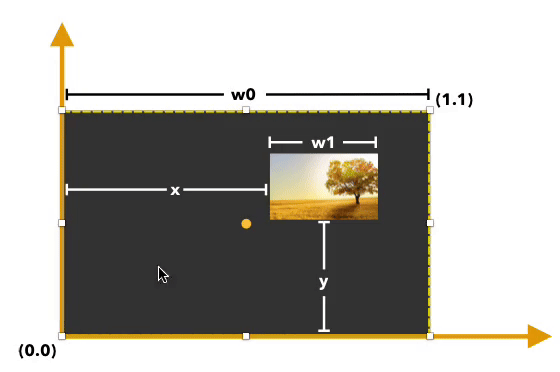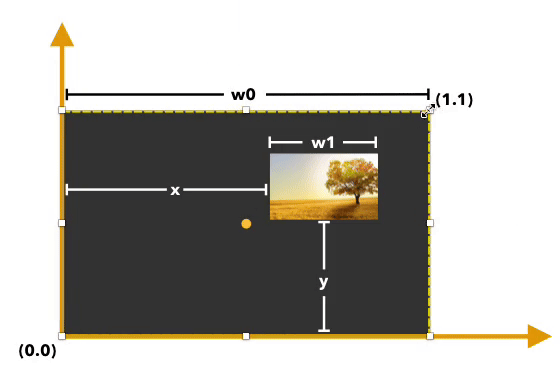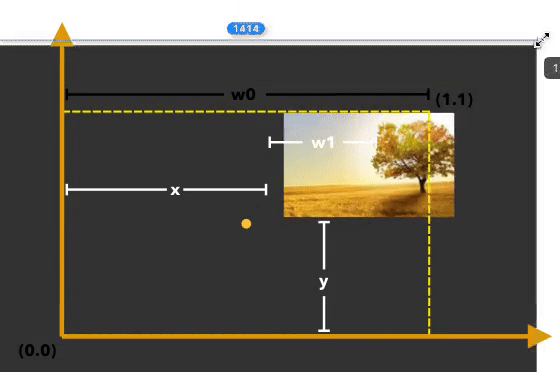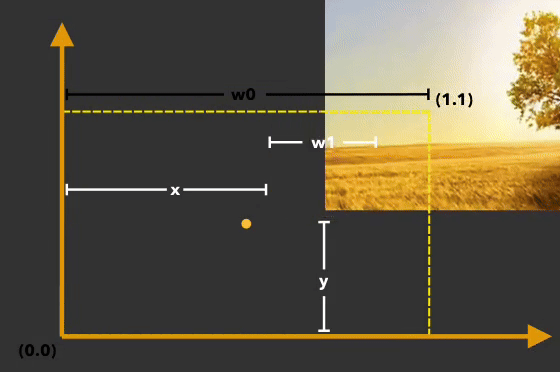
You have a canvas with width w0 and an image with width w1. Both have the same aspect ratio. The image is initially inside the canvas, but offset from the bottom-left corner by (x, y). What should the pivot point be in order to scale the image to perfectly fill the canvas?

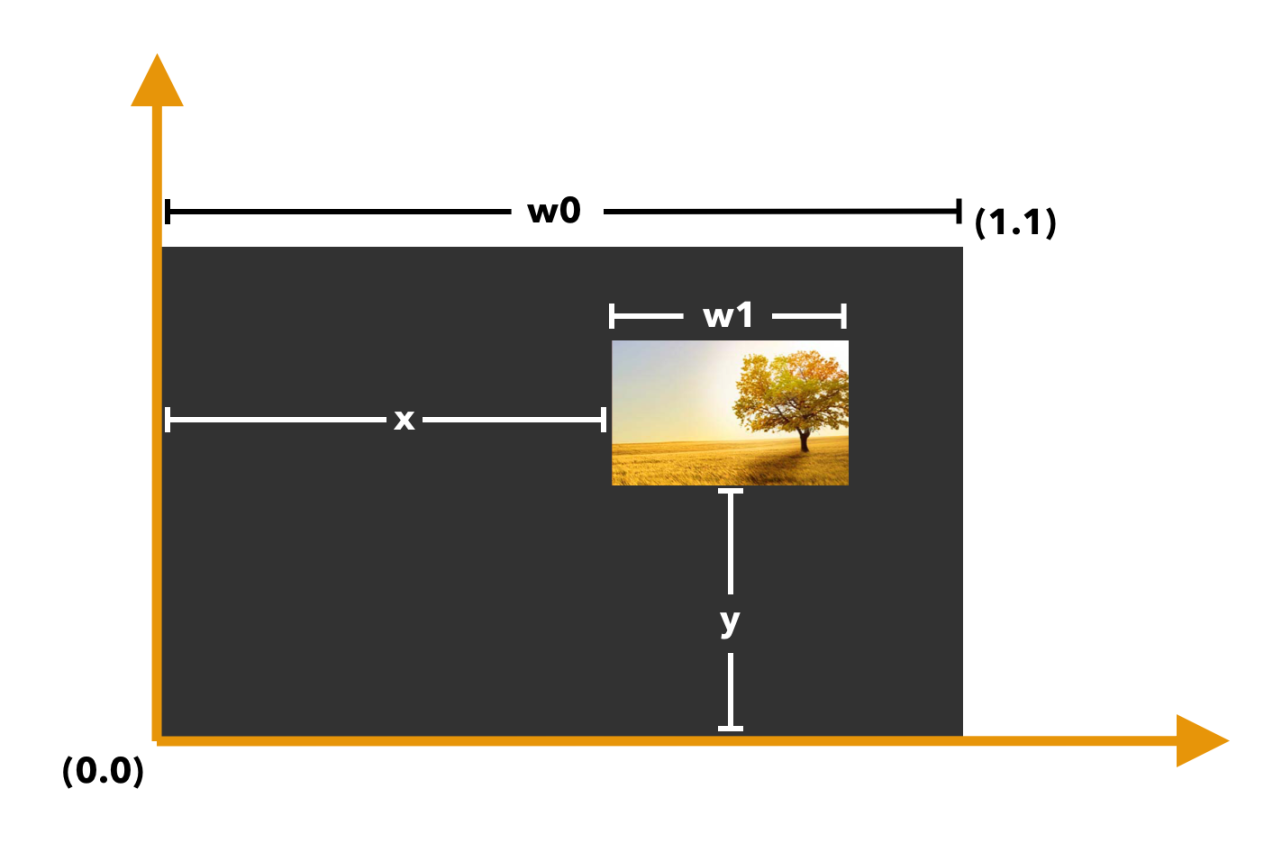
In the above example, if the pivot point was directly in the middle of the canvas, the image would expand far to the top-right instead of filling the canvas.

Initial thoughts

A reasonable guess is that the pivot should be inside the image such that it's at the same place the centre of the image is in the canvas. If the center of the image is x% of the way across the canvas, you’d put the pivot point x% of the way across the image, and do the same for y. I'll refer to this method as the proportional point.

Essentially, the goal is to map the corners of the image to the corners of the canvas. To do this, the pivot point must be along the line connecting the two corners (if you extend it into the image). By drawing two of these lines, you can find the pivot point at the intersection.

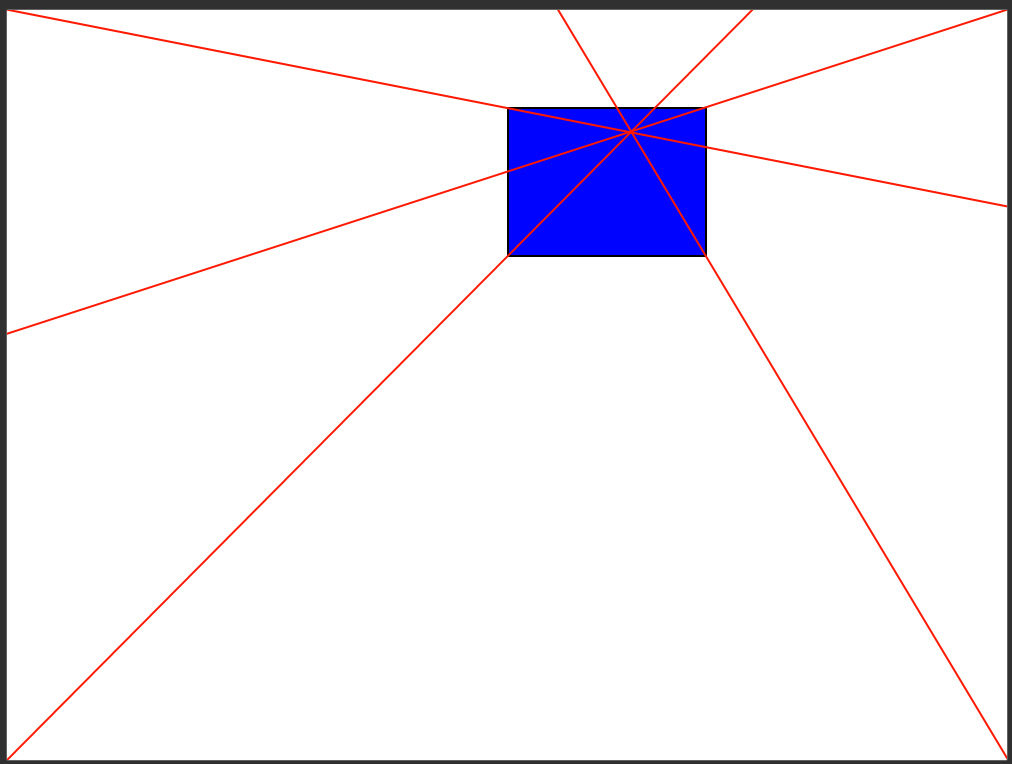(Illustration by Tiger64.)

However, it's not clear that the intersection of these lines is the proportional point.

An issue is discovered

The proportional point doesn't work for the corners. If the image is snug against a corner of the canvas, the pivot point should be at the corner. This makes sense intuitively and matches with the line intersection method, but the proportional point is a little distance away from the corner.

A cool Desmos visualization was made by Tiger64 to illustrate this discrepancy. The red dot is the center of the image, the blue dot is the point in the image where the image is in the canvas, and the purple dot is the actual pivot point. (Note that there is a slight change in variables: (x0, y0) is the centre of the image, not the bottom-left corner.)

Finding the intersection of the lines is just solving a system of two equations. This formula is reached, which is not quite as simple as the proportional point.

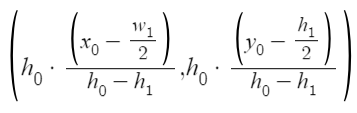
The problem author indicates that this is correct (provided the heights are known), but shares a different method of reaching the answer.

Fun with geometric series

Instead of only applying the proportional point once, it's repeatedly applied until the point converges.

For any scale s = w1/w0, the formula for the infinite geometric series:
S = 1 + s + s^2 + s^3 + ... = 1/(1-s).

There's a simple proof of this:

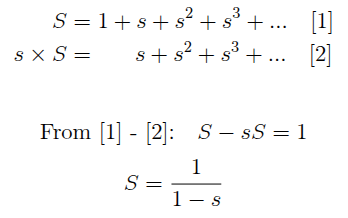
Then you get the center of the inner image c as a fraction of w0 and w1, and calculate pivot proportion = 0.5 + (c - 0.5) * 1 / (1 - s), and multiply along w0 or w1.

For example, with w1/w0 being 1/4 and c = (0.7, 0.7):

• the sum is 1 + 1/4 + 1/16 + 1/64 + ... = 4/3, and
• the pivot proportion should therefore be (0.766.., 0.766..).

Eventually, a few of us manage to simplify it to the following (equivalent) solution.

Let s = w0/(w0-w1). Then the pivot point should be (s*x, s*y), where (x, y) is the bottom-left corner of the image.

Result