Memoization and Dynamic Programming

One of the computer science concepts that took me a long time to learn was dynamic programming, or DP. Like many things in computer science, the name sounds cool but provides little explanation to what it is (see: monads).

Dynamic programming is a technique for solving problems that have optimal substructure. This means that an optimal solution can be found by combining optimal solutions to sub-problems which have the same structure as the original problem. Typically, the initial sub-problems are very simple so the optimal solution can be found trivially. This is a "bottom-up" solution, since we start with easy problems at the "bottom" before building to the "top".

A related concept is memoization (not "memorization"). Memoization involves caching the result of a function based on its parameters, so that any internal computational work doesn't need to be repeated if it's called again. The memoized function must be referentially transparent: it should always return the same value when called with the same parameters, otherwise the cache would return the wrong answer!

A problem that can be solved using DP can also be solved using memoization, with minor runtime differences if any. In the memoization solution, we write a recursive function that attempts to solve the entire problem, and recursively break it down into smaller problems until we reach the base case (some trivial subproblem). We cache the results of every call to this recursive function so that after we solve a subproblem in one branch, we don't need to solve it again. This is a "top-down" approach, since we start with the big problem at the top and break it down.

My experience with DP is that it's very difficult to come up with the correct "way" of building the subproblems into the original problem. Instead, it's much easier for me to write a recursive solution first, and then memoize it.

Day 19 of Advent of Code 2024 was such a problem that could be solved using DP or memoization.

Day 19: Linen Layout

We are given a set of towels with coloured stripes (e.g. r, wr, b, g, bwu, rb, gb, br) and a set of desired patterns (e.g. brwrr, bggr, ubwu). We need to identify how many ways each pattern can be built, using the towels we have. Towels can be used more than once.

For example:

• brwrr can be made 2 ways: b, r, wr, r or br, wr, r
• bggr can only be made 1 way: b, g, g, r
• ubwu can't be made at all

Naive Solution

Let's start with brwrr. If I were doing this manually, I would first look for all the towels that start with the same letters as the desired pattern (i.e. have the same prefix) and then try filling in the rest of the letters for each one. So b and br are possible starting towels.

If we start with towel b, then we have rwrr left, and we can repeat this process. The only towel that has the same prefix is r, which leaves us with wrr. Again, the only towel that has the same prefix is wr, which leaves us with the final towel r.

If we start with towel br and go through the same algorithm, we will find that the only towels we can use are wr and r.

Now, since we know that any solution to brwrr must start with b or br (no other towels share a prefix), we can simply add up the number of ways we've gotten above to get the total number of ways. This is 1 + 1 = 2 ways.

Notice the recursive structure of the algorithm. If a function F can solve our problem, then we can implement it by finding all the towels that share a prefix with the desired pattern, and then for each one, subtracting the shared prefix and then calling F again with the remaining letters. These are our subproblems. Once we have the answers to those, we add them up to get the answer to a bigger problem.

The base case is an empty towel "", which can only be built 1 way.

Improving the Algorithm

This works, but is very slow. We can identify that this problem has optimal substructure, so DP or memoization are good ways to tackle it.

Rather than think of how to build the DP solution, we can simply memoize our buildWays() function. For example, once we find out that rwrr can only be made 1 way, we can cache rwrr -> 1. If we ever need to find how many ways rwrr can be made again, then we can just grab it from the cache.

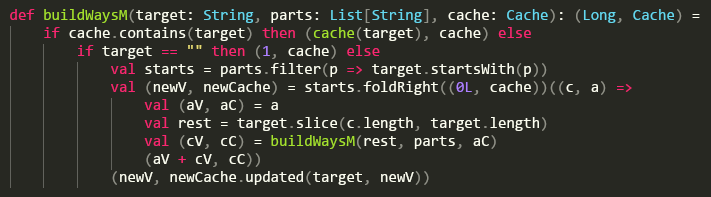(Because I'm writing this functionally, I need to pass around the cache so that every call gets the updated cache. A much simpler way would be to have the cache be a global variable.)

This reduces the runtime significantly and produces the correct answer in less than a second.

If you're wondering how the DP solution would look, here's a sketch.

You'll want to have a list of all constructions of some prefix of the desired pattern. Then you increase the size of the prefix by 1, and check if it's possible to create the new prefix for each of the existing constructions using 1 new towel. Repeat until the entire desired pattern is created.

For the example brwrr:

1. The prefix '' can be created using an empty string. [list holds '']
2. The prefix b can only be created by adding the b towel to the empty string. [list holds '', b]
3. The prefix br can be created by adding r to the b construction, or by adding br to the empty string. [list holds ['', b, b+r, br]
4. The prefix brw can't be created from any of the existing constructions.
5. The prefix brwr can be created by adding wr to the b+r construction, and wr to the br construction. [list holds '', b, b+r, br, b+r+wr, br+wr]
6. The prefix brwrr can be created by adding r to b+r+wr or br+w. [list holds '', b, b+r, b+r+wr+r, br+wr+r]

And then we've reached the original problem, so there are 2 ways of forming brwrr. Notice how we're using the optimal solution to every smaller prefix in order to create the solution to the current prefix,. Our solution will always be optimal since it's not possible to create the current prefix without using some earlier prefix, which we already found the optimal solution for.

This can be optimized by mapping the constructions to the prefix they create, since it doesn't matter how the constructions are internally formed for a particular prefix: they'll always be able to form the next prefix in the same way (if possible). For example, it didn't matter that br could be created using b+r or br: both of them create brwr by adding wr.