The lambda calculus is like a "minimal" form of a functional programming language. By using only anonymous functions of 1 variable and function application, an entire programming language can be derived. Note that this will not be a rigorous definition. Instead, I'm hoping it's an intuitive introduction to some of the concepts.
Since the functional languages I'm most familiar with are Haskell and Clojure, I'll be using some variation of their syntax (which is slightly different from how it's typically written). An expression in lambda calculus has the following grammar:
var = x | y | ...expr = var | fn_definition | fn_applicationfn_definition = (λvar -> expr)fn_application = (expr expr)
Parentheses are used to enclose a function definition and to express function application, like in a Lisp. Thus, (f a) is the expression a applied to f, which might be written as f(a) in some languages.
That's it! Observe the conspicuous absence of numbers, booleans, operators, if-statements, loops/recursion and data structures. We'll be deriving a system that implements all of those. However, we'll need to cover some ground concepts first to help with terminology and notation.
First-class functions
If you're familiar with any modern programming language, you're probably aware that functions can be treated just like values, in that they can be passed around like variables. We can thus have a function that returns another function, and we can pass in either a variable or an entire function. (We'll be exploring the untyped lambda calculus, which means anything can be accepted.) This means that you'll see expressions like:
((λy -> (λx -> y)) (λa -> a)).
It's important not to get lost in the parentheses; it might help to write these down on a separate piece of paper when trying to work them out. This is also why the fn_application rule is defined as (expr expr) and not (fn_definition expr). Since the result of a function application can be another function, we can use that as the first argument of a function application!
All functions in lambda calculus are anonymous, and due to the lack of an assignment operator, we cannot give any of them names. However, to avoid re-treading over concepts as we build upon our work, I'll name particular functions so that they're easy to recognize and it'll also reduce the length of our expressions. However, this is just shorthand: we must always be able to expand or transform such named functions into their full form. In particular, we cannot implement recursion using a named function, since it would expand forever.
Reduction
An expression in lambda calculus can be reduced by following normal function application rules. For example, (λy -> y) is the identity function: it takes in an input and returns it unchanged. The expression
((λy -> y) x) (the variable x applied to the identity function)
thus can be reduced to x. Essentially, when we apply an expression to a function definition, we can replace all instances of the parameter with the expression.
If we were to reduce the earlier expression:
((λy -> (λx -> y)) (λa -> a))
This is (λa -> a) applied to (λy -> (λx -> y)), so we can reduce this to (λx -> (λa -> a)).
Here's another example. Try reducing:
(((λx -> (λy -> x)) a) b).
Applying a to the innermost function results in ((λy -> a) b), and applying b to that function results in just a.
Free variables
In an expression, a variable is free if it is not bound in any enclosing function definition's parameter (we could say that it is undefined). For example,
- the expression
(λy -> x)has a free variablex, since the enclosing function only bindsyas its parameter. - the expression
(λx -> (λy -> (x y)))has no free variables, since bothxandyare defined in enclosing functions.
Lambda calculus uses lexical scoping: that means that a variable is bound to the innermost function definition that has it as a parameter. In other words, it means we can write:
(λx -> ((λy -> (λx -> (y x))) x))
and the innermost x is bound to the innermost function definition, and can be different from the outermost x (i.e. it works intuitively). However, to avoid confusion, I'll just always use different variable names.
All of our top-level expressions should not have any free variables, or else the expression cannot be evaluated.
Currying
Currying is a technique for defining functions that take more than one parameter. This is done by defining a function that accepts 1 parameter, which returns another function that accepts another parameter (optionally continue in this fashion), which then returns the result. This is how functions in Haskell work.
For example, we can write a curried function that computes the area of a rectangle as below (in JS):
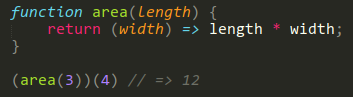
Do stare at the example until it makes sense, since it can be weird to think about at first. In lambda calculus (assuming we had implemented * as multiplication somehow), we would express such a function as (λl -> (λw -> (* l w))). Interestingly, this allows us to easily define partially applied functions. For example, area(2) returns a function that calculates the area of any 2xN rectangle, and can be reused on its own.
Since we'll be using functions like this frequently, I'll express a function that "takes 2 variables" as (λx,y -> expr). However, remember that this is just shorthand, and can always be decomposed to (λx -> (λy -> expr)). In a similar manner, I'll express the application of two variables x and y to such a function as (f x y), even though this is just shorthand for ((f x) y).
Now that we've gotten the groundwork out of the way, we can start exploring how to implement a programming language! The next entry will start with the implementation of natural numbers using Church numerals.